Class 10 Model activity task math 2021 new বা দশম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক 2021 এর সমস্ত প্রশ্ন উত্তর নিয়ে আজকের পর্বে আমরা আলোচনা করব। এর আগেও আমরা 2020 সালের দশম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক এর উত্তর প্রকাশ করেছিলাম যা তোমাদের খুবই পছন্দ হয়েছিল। তাই এবারও আমরা দশম শ্রেণীর গণিত মডেল অ্যাক্টিভিটি টাস্ক 2021 (Model Activity Task class 10 mathematics part 4 )নিয়ে আলোচনা করছি। আশা করি তোমাদের এবারও পছন্দ হবে। তাহলে চলো শুরু করা যাক:
Class 10 model activity task Mathematics 2021 new
দশম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট 4 2021
গণিত মডেল অ্যাক্টিভিটি টাস্ক 2021
গণিত (Mathematics)
দশম শ্রেণি
নিচের প্রশ্নগুলির উত্তর লেখ :
1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQ)
(i) বাস্তব সহগ যুক্ত একচলবিশিষ্ট দ্বিঘাত সমীকরণটি হল
(a) $x\left( {{x}^{2}}-1 \right)-3x=0$ (b) ${{x}^{2}}({{x}^{2}}-1)-6x=0$ (c) x(x-1)-x=0 (d) $2x-4=0$
উত্তর: (c) $x(x-1)-x=0$
(ii) (2x-2)(x+3)=0 সমীকরণটির বীজ দুটি হলো
(a) -1,-3 (b) -1,3 (c) 1,-3 (d) 1,3
উত্তর: (c) 1,-3
(iii) বার্ষিক 10% সরল সুদের হারে 50 টাকার 2 বছরের সুদ ঐ একই হারে 100 টাকার 1 বছরের সুদের
(a) দ্বিগুণ (b) অর্ধেক (c) এক চতুর্থাংশ (d) সমান
উত্তর: (d) সমান
(iv) O কেন্দ্রীয় বৃত্তের PQ ও RS দুটি সমান দৈর্ঘ্যের জ্যা । O বিন্দু থেকে PQ জ্যা এর দূরত্ব 8 সেমি. হলে , O বিন্দু থেকে RS জ্যা এর দূরত্ব কত?
উত্তর: 8 সেমি ।
সমাধানঃ ত্রিভুজের কেন্দ্র থেকে জ্যা এর দূরত্ব বলতে লম্ব দূরত্ব বোঝায়। অর্থাৎ , $OC\bot PQ$ এবং $OD\bot RS$
OQ = OS (এরা একই বৃত্তের ব্যাসার্ধ)
$CQ=\frac{1}{2}PQ=\frac{1}{2}RS=DS$ (PQ ও RS দুটি সমান দৈর্ঘ্যের জ্যা)
$\vartriangle COQ$ ও $\vartriangle ODS$ এর
$\angle OCQ=ODS=90{}^\circ $
OQ=OS
CQ=DS
$\therefore $ $\vartriangle COQ$ ও $\vartriangle ODS$ পরস্পর সর্বসম।
$\therefore $ OC=OD=8 সেমি ।
ক্লাস টেন গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট 4 new 2021
2. সত্য / মিথ্যা লেখ (T/F)
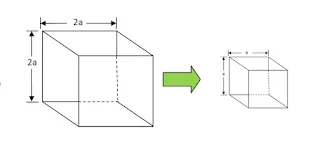
(i) একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য অর্ধেক করা হলে , ঘনকটির আয়তন প্রথম আয়তনের $\frac{1}{8}$ অংশ হবে।
উত্তর: সত্য (T) ।
সমাধানঃ
ধরি ঘনকটির প্রাথমিক বাহুর দৈর্ঘ্য ছিল 2a । অর্থাৎ অন্তিম দৈর্ঘ্য ছিল a ।
আমরা জানি , ঘনকের আয়তন = (বাহু)3
অতএব, প্রাথমিক আয়তন= (2a)3 = 8a3
এবং , অন্তিম আয়তন =(a)3 = a3
এখন,( অন্তিম আয়তন ÷ প্রাথমিক আয়তন) = $\frac{{{a}^{3}}}{8{{a}^{3}}}=\frac{1}{8}$
(ii) $\frac{a}{2}=\frac{b}{3}=\frac{c}{4}$ হলে , a:b:c=4:3:2 হবে।
উত্তর: মিথ্যা (T)।
সমাধানঃ
ধরি, $\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k$
বা, a=2k , b=3k , c=4k
এখন, a:b:c=2k:3k:4k = 2:3:4
(iii) আসল P টাকা এবং বার্ষিক চক্রবৃদ্ধি সুদের হার r% হলে , দ্বিতীয় বছরের মূলধন $\frac{Pr}{100}$ টাকা।
উত্তর: মিথ্যা (T) ।
সমাধান, দ্বিতীয় বছরের মূলধন =আসল + প্রথম বছরের সুদ।
দ্বিতীয় বছরের মূলধন = $P{{\left( 1+\frac{r}{100} \right)}^{1}}$
= $P+\frac{Pr}{100}\ne \frac{Pr}{100}$ ( কারণ , $P\ne 0$ )
(iv) চিত্রে O কেন্দ্রবিশিষ্ট বৃত্তে AB একটি ব্যাস । বৃত্তের ভেতরে Q একটি বিন্দু । $\angle AQB$ সর্বদা সূক্ষ্মকোণ ।
উত্তর: মিথ্যা (T) ।
সমাধান:
অঙ্কনঃ AQ কে বর্ধিত করলাম যা বৃত্তের পরিধিকে K বিন্দুতে ছেদ করল। R,B যুক্ত করলাম ।
প্রমাণঃ $\angle ARB=90{}^\circ $ ( অর্ধবৃত্তস্থ কোন)
$\therefore \angle RQB+\angle RBQ=90{}^\circ $
$\therefore \angle RQB=90{}^\circ -\angle RBQ$
$\therefore \angle RQB<90{}^\circ $ ($\angle RBQ\ne 0$)
$\therefore \angle AQB=180{}^\circ -\angle RQB$
$\therefore \angle AQB>90{}^\circ $ (প্রমাণিত)
আরও পড়ো: | 2020 দশম শ্রেণী জীবন বিজ্ঞান মডেল অ্যাক্টিভিটি টাস্ক পার্ট 1 । Class 10 Math model activity part 1
আরও পড়ো: | 2020 দশম শ্রেণী জীবন বিজ্ঞান মডেল অ্যাক্টিভিটি টাস্ক পার্ট 2 । Class 10 Math model activity part 2
আরও পড়ো: | 2020 দশম শ্রেণী জীবন বিজ্ঞান মডেল অ্যাক্টিভিটি টাস্ক পার্ট 3 । Class 10 Math model activity part 3
3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (SA):
(i) একটি লম্ববৃত্তাকার চৌঙের আয়তন এবং বক্রতলের ক্ষেত্রফল সংখ্যামানে সমান হলে , উহার ব্যাসার্ধ নির্ণয় কর।
সমাধানঃ
লম্ব বৃত্তাকার চৌঙের আয়তন $=\pi {{r}^{2}}h$
লম্ব বৃত্তাকার চৌঙের বক্রতলের ক্ষেত্রফল \[=2\pi rh\]
শর্তানুসারে, $\not{\pi }{{r}^{2}}\not{h}=2\not{\pi }r\not{h}$
বা, $\frac{{{r}^{2}}}{r}2$
উত্তরঃ চৌঙটির ব্যাসার্ধ 2 একক ।
(ii) দেখাও যে, মিশ্র দ্বিঘাত করণী $(7-\sqrt{2})$ এর অনুবন্ধী করণী হলো $(7+\sqrt{2})$ ।
সমাধানঃ
কোনো করণী ও তার অনুবন্ধী করণীর গুনফল সর্বদা একটি মুলদ সংখ্যা হবে।
এক্ষেত্রে, $(7-\sqrt{2})(7+\sqrt{2})$
= ${{7}^{2}}-{{(\sqrt{2})}^{2}}$=49-2 =47
অতএব $(7-\sqrt{2})$ এর অনুবন্ধী করণী হলো $(7+\sqrt{2})$ ।
Model Activity Task class 10 mathematics part 4 new 2021
4. যুক্তি দিয়ে প্রমান কর যে বৃত্তস্থ চতুর্ভুজের বিপরিত কোণগুলি পরস্পর সম্পুরক।
সমাধানঃ
প্রদত্ত: O কেন্দ্রীয় বৃত্তে PQRS একটি বৃত্তস্থ চতুর্ভুজ।
প্রমান্য বিষয়ঃ $\angle PQR+\angle PSR$ =2 সমকোণ ।
অঙ্কনঃ P , O এবং R , O যুক্ত করলাম।
প্রমাণঃ PSR বৃত্তচাপের দ্বারা গঠিত কেন্দ্রস্থ প্রবৃদ্ধ কোণ $\angle POR$ এবং বৃত্তস্থ কোণ $\angle PQR$
$\therefore $ প্রবৃদ্ধ $\angle POR$ =2$\angle PQR$
$\therefore \angle PQR=\frac{1}{2}$ প্রবৃদ্ধ $\angle POR$ …. (i)
আবার , PQR দ্বারা গঠিত কেন্দ্রস্থ প্রবৃদ্ধ কোণ $\angle POR$ এবং বৃত্তস্থ কোণ $\angle PSR$
$\therefore $ প্রবৃদ্ধ $\angle POR$ =2$\angle PSR$
$\therefore \angle PSR=\frac{1}{2}\angle POR$ …. (ii)
(i) ও (ii) থেকে পাই , $\angle PQR+\angle PSR$ = $\frac{1}{2}$ প্রবৃদ্ধ $\angle POR$$+\frac{1}{2}\angle POR$
= $\frac{1}{2}\times $ 4 সমকোণ = 2 সমকোণ। ( প্রমাণিত )
Class 10 Model activity task math 2021 new
Mocktest | দশম শ্রেণী অধ্যায় বংশগতি মক টেস্ট | জীবন বিজ্ঞান | Class 10 Life science Heredity Mock Test
আশা করি আজকের এই পর্বের উত্তর তোমাদের পছন্দো হয়েছে। ভালো লাগে তাহলে অবশ্যই বন্ধুদের সাথে শেয়ার করতে ভুলবে না। আমাদের টেলিগ্রাম গ্রুপে যুক্ত হওয়া আর আরো বেশি পড়াশোনা বিষয়ক সামগ্রী পাও। ছাত্রছাত্রীরা বাড়িতে নিজের বিষয়ভিত্তিক খাতায় এগুলো করে বিদ্যালয় খুললে শিক্ষকের কাছে জমা দেবে।
কোনো অবস্থাতেই তারা বাড়ির বাইরে বেরোবে না।