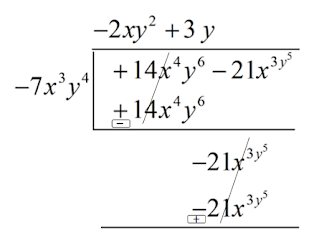সপ্তম শ্রেণির গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট ৮ নিয়ে আজকের পর্বে আমরা আলোচনা করব ।
নিচের প্রশ্নগুলির উত্তর লেখঃ
১. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQ)
(i) কোনটি ত্রিভুজের সর্বসমতার শর্ত নয় –
(a) বাহু-বাহু-বাহু (b) বাহু-কোণ-বাহু (c) কোণ-কোণ-বাহু (d) কোণ- কোণ–কোণ
উত্তরঃ (d) কোণ- কোণ–কোণ
ii) $\frac{4}{49}$ বর্গসেমি ক্ষেত্রফল বিশিষ্ট বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য হবে
(a) $\sqrt{\frac{4}{49}}$ সেমি (b) $\frac{2}{7}$ সেমি (c) 2 সেমি (d) 7 সেমি
উত্তরঃ (b) $\frac{2}{7}$ সেমি
iii) 1.69 এর বর্গমূল হল -
(a) 13 (b) 1.3 (c) 0.13 (d) 13.03
উত্তরঃ (b) 1.3
iv) xy=
(a) ${{\left( x+y \right)}^{2}}-{{\left( x-y \right)}^{2}}$
(b) ${{\left( x+y \right)}^{2}}+{{\left( x-y \right)}^{2}}$ 1.3
(c) ${{\left( \frac{x+y}{2} \right)}^{2}}+{{\left( \frac{x-y}{2} \right)}^{2}}$
(d) ${{\left( \frac{x+y}{2} \right)}^{2}}-{{\left( \frac{x-y}{2} \right)}^{2}}$
উত্তরঃ (d) ${{\left( \frac{x+y}{2} \right)}^{2}}-{{\left( \frac{x-y}{2} \right)}^{2}}$
(i) যখন কোনো ট্রেন সেতু অতিক্রম করে তখন ট্রেনটিকে অতিক্রম করতে হবে −
(a) ট্রেনটির নিজের দৈর্ঘ্য (b) সেতুর দৈর্ঘ্য (c) ট্রেনটির নিজের দৈর্ঘ্য + সেতুর দৈর্ঘ্য (d) সেতুর দৈর্ঘ্য − ট্রেনটির নিজের দৈর্ঘ্য
উত্তর: (c) ট্রেনটির নিজের দৈর্ঘ্য + সেতুর দৈর্ঘ্য
(ii) ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল =
(a) (বাহুর দৈর্ঘ্য)² (b) বাহুগুলির দৈর্ঘ্যের সমষ্টি (c) $\frac{1}{2}$(ভূমির দৈর্ঘ্য + উচ্চতা) (d) $\frac{1}{2}$ভূমির দৈর্ঘ্য × উচ্চতা
উত্তর: (d) $\frac{1}{2}$ভূমির দৈর্ঘ্য × উচ্চতা
(iii) a²−b² =
(a) (a+b)² (b) (a-b)² (c) (a+b) (a-b) (d) (a+b)² + (a-b)²
উত্তর: (c) (a+b)(a-b)
(iv)
রাস্তাসহ জমির দৈর্ঘ্য এবং রাস্তা বাদে জমির প্রস্থ হলো যথাক্রমে
(a) 23 মি., 21 মি. (b) 29 মি., 21 মি. (c) 26 মি., 21 মি. (d) 26 মি., 15 মি.
উত্তর: (d) 26 মি., 15 মি.
2. সত্য / মিথ্যা লেখো ( T / F ):
i) ${{(x+y)}^{2}}$ - এর সুত্র থেকে ${{(x-y)}^{2}}$ এর সুত্র নির্ণয় করতে y এর পরিবর্তে (-y) লিখতে হবে।
উত্তরঃ ঠিক ।
ii) $\left( 4-x \right)\left( x-4 \right)=16-{{x}^{2}}$
উত্তরঃ ভুল ।
কারনঃ
প্রদত্ত বামপক্ষঃ $\left( 4-x \right)\left( x-4 \right)=16-{{x}^{2}}$
$=4x-16-{{x}^{2}}-4x$
$=-16-{{x}^{2}}$
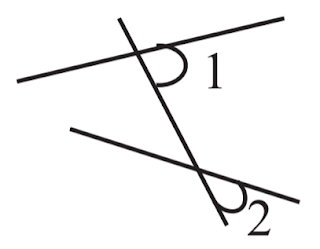
iii)
চিত্রে $\angle 1$ ও $\angle 2$ পরস্পর অনুরূপ কোণ ।
উত্তরঃ ভূল ।
iv)
চিত্রে , বিষমবাহু $\Delta ABC$ - এর একটি উচ্চতা AD । AD ত্রিভুজটির একটি মধ্যমা
উত্তরঃ ভূল ।
(v) দুটি স্তম্ভ চিত্রকে পাশাপাশি এঁকে দুটি তথ্য সহজে তুলনা করার জন্য যে চিত্র আঁকা হয় সেই চিত্রটি হলো দ্বিস্তম্ভ লেখ ।
উত্তর: সত্য
(vi) প্রথম ট্রেনের গতিবেগ x কিমি./ঘন্টা এবং দ্বিতীয় ট্রেনের গতিবেগ y কিমি./ঘন্টা । ট্রেন দুটি পরস্পর বিপরীত দিকে চললে 1 ঘন্টায় মোট যাবে (x-y) কিমি. ।
উত্তর: মিথ্যা
(vii)
চিত্রে ∠1 ও ∠2 কোণ জোড়কে একান্তর কোণ বলা হয়।
উত্তর: মিথ্যা
(viii) x এর যেকোনো মানের জন্য, (x+5)(x+3)=x²+8x+15 −এর সমান চিহ্নের দুপাশে মান সমান হয় । তাই এটি একটি অভেদ ।
উত্তর: সত্য
2. সত্য মিথ্যা লেখ (T/F)
i) ${{(x+y)}^{2}}$ - এর সুত্র থেকে ${{(x-y)}^{2}}$ এর সুত্র নির্ণয় করতে y এর পরিবর্তে (-y) লিখতে হবে।
উত্তরঃ ঠিক ।
ii) $\left( 4-x \right)\left( x-4 \right)=16-{{x}^{2}}$
উত্তরঃ ভুল ।
কারনঃ
প্রদত্ত বামপক্ষঃ $\left( 4-x \right)\left( x-4 \right)=16-{{x}^{2}}$
$=4x-16-{{x}^{2}}-4x$
$=-16-{{x}^{2}}$
iii)
চিত্রে $\angle 1$ ও $\angle 2$ পরস্পর অনুরূপ কোণ ।
উত্তরঃ ভূল ।
iv)
চিত্রে , বিষমবাহু $\Delta ABC$ - এর একটি উচ্চতা AD । AD ত্রিভুজটির একটি মধ্যমা
উত্তরঃ ভূল ।
ক্লাস সেভেন অংক মডেল অ্যাক্টিভিটি পার্ট 8
3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন
i) গনিতের ভাষায় সমস্যাটি হল,
| সময় (মিনিট) | দূরত্ব (মিটার) |
|---|---|
| 1 | 150 |
| 25 | x |
গতিবেগ একই থাকলে সময় ও দূরত্বের সমানুপাতি সম্পর্কের সাহায্যে x এর মান নির্নয় কর ।
সমাধানঃ
শর্তানুসারে , 1:150 = 25: x
বা , $\frac{1}{150}=\frac{25}{x}$
বা , $x=150\times 25=3750$
উত্তরঃ x এর মান 3750 মিটার ।
ii)
তালিকাটির সাহায্যে একটি দ্বিস্তম্ভ লেখছিত্র অঙ্কন কর।
| বছর | 2009 | 2010 |
|---|---|---|
| পড়ার বই | 1200 | 800 |
| গল্পের বই | 1400 | 1100 |
iii) $m+\frac{1}{m}=-P$ হলে , দেখাও যে , ${{m}^{2}}+\frac{1}{{{m}^{2}}}={{P}^{2}}-2$
সমাধানঃ
বামপক্ষ = ${{m}^{2}}+\frac{1}{{{m}^{2}}}$ = ${{(m)}^{2}}+{{\left( \frac{1}{m} \right)}^{2}}$
= ${{(m)}^{2}}+{{\left( \frac{1}{m} \right)}^{2}}+2.m.\frac{1}{m}-2.\not{m}.\frac{1}{{\not{m}}}$
= ${{\left( m+\frac{1}{m} \right)}^{2}}-2$ = ${{P}^{2}}-2$ = ডানপক্ষ
(iv) √2 এর দুই দশমিক পর্যন্ত আসন্ন মান নির্ণয় করো ।
সমাধানঃ
1 ) 2.0000 ( 1.414
1
24)100(
96
281)400(
281
2824)11900(
11296
604
∴ √2 = 1.414 (প্রায় )
উত্তরঃ √2 = 1.41 (দুই দশমিক স্থান পর্যন্ত আসন্নমান)
(v) ত্রিভুজের সর্বসমতার শর্তগুলি লেখো ।
উত্তর: ত্রিভুজের সর্বসমতার শর্তগুলি হলো :
- (i) বাহু-বাহু-বাহু বা S-S-S
- (ii) বাহু-কোণ-বাহু বা S-A-S
- (iii) কোণ-কোণ-বাহু বা A-A-S
- (iv) সমকোণ-অতিভুজ-বাহু বা R-H-S
(vi) x+y=5 এবং x−y=1 হলে, 8xy(x2+y2) এর মান নির্ণয় করো ।
সনাধানঃ
$8xy\left( {{x}^{2}}+{{y}^{2}} \right)$
$=4xy.2\left( {{x}^{2}}+{{y}^{2}} \right)$
$=\{{{(x+y)}^{2}}-{{(x-y)}^{2}}\}.\{{{(x+y)}^{2}}+{{(x-y)}^{2}}\}$
$=({{5}^{2}}-{{1}^{2}})({{5}^{2}}+{{1}^{2}})$
$=(25-1)(25+1)$
$=24\times 26$
=624
উত্তরঃ $8xy\left( {{x}^{2}}+{{y}^{2}} \right)$ এর মান 624
4. i. সংখ্যারেখায় (6) + (-2)-কে দেখাও।
ii. প্রথম বীজগাণিতিক সংখ্যামালাকে দ্বিতীয় বীজগাণিতিক সংখ্যামালা দিয়ে ভাগ করে ভাগফল নির্ণয় করো: $14{{x}^{4}}{{y}^{6}}-21{{x}^{3{{y}^{5}}}}\ ,\ -7{{x}^{3}}{{y}^{4}}$ যেখানে $x\ne 0,y\ne 0$
সমাধানঃ
5 (i) ABC একটি ত্রিভুজ আঁকো যার BC = 5.5 সেমি, ∠ABC=60° ও∠ACB=60°
সমাধানঃ
বিঃ দ্রঃ - কিভাবে আঁকা হয়েছে তা নিচের ভিডিওতে বোঝানো হয়েছে।
(ii) করিমচাচা আয়তক্ষেত্রাকার জমির দৈর্ঘ্য প্রস্থের 2 গুণ এবং এই জমির ক্ষেত্রফল 578 বর্গমিটার । করিমচাচা জমিটির দৈর্ঘ্য , প্রস্থ ও পরিসীমা নির্ণয় করো।
সমাধানঃ ধরি করিমচাচা আয়তক্ষেত্রাকার জমির প্রস্থ x মিটার।
অতএব , ওই জমির দৈর্ঘ্য 2x মিটার।
অর্থাৎ, ওই জমির ক্ষেত্রফল $(x\times 2x)$ বর্গমিটার = $2{{x}^{2}}$ বর্গমিটার।
শর্তানুসারে , $2{{x}^{2}}=578$
বা, ${{x}^{2}}=\frac{578}{2}=289$
বা , $x=\sqrt{289}$
বা , x=17
অর্থাৎ, জমিটির প্রস্থ 17 মিটার
▣ জমিটির দৈর্ঘ্য $(17\times 2)$ মিটার = 34 মিটার ।
উত্তরঃ জমিটির পরিসিমা $2(34+17)$ মিটার = $2\times 51$ মিটার = 102 মিটার।
(iii) 90 মিটার লম্বা একটি রেলগাড়ি একটি স্তম্ভকে 25 সেকেন্ডে অতিক্রম করলো। রেলগাড়ি গতিবেগ ঘন্টায় কত কিলোমিটার নির্ণয় করো ।
উত্তর: 1 ঘন্টা = 3600 সেকেন্ড
1000 মিটার = 1 কিমি.
গণিতের ভাষায় সমস্যাটি হলো :
সময় (সেকেন্ড) দূরত্ব (মিটার)
25 90
3600 ?
এক্ষেত্রে সময় বাড়লে ট্রেনটি বেশি দূরত্ব অতিক্রম করবে |
তাই, সময় ও দূরত্বের মধ্যে সরল সম্পর্ক |
∴ সমানুপাতটি হবে,
25 : 3600 : : 90 : নির্ণেয় দূরত্ব
∴ নির্ণেয় দূরত্ব $\frac{\overset{144}{\mathop{\not{3}\not{6}\not{0}\not{0}}}\,\times 90}{\not{2}\not{5}}$ =12960 মিটার = 12.96 কিমি.
∴ রেলগাড়িটি 3600 সেকেন্ড অর্থাৎ 1 ঘন্টায় 12.96 কিমি. দূরত্ব অতিক্রম করে |
∴ রেলগাড়িটির গতিবেগ 12.96 কিমি./ঘন্টা |