Class 10 mathematics part 8 mark 50 model activity task | দশম শ্রেণী গণিত পার্ট ৮ মডেল অ্যাক্টিভিটি টাস্ক মার্ক ৫০ | ক্লাস টেন ম্যাথ পার্ট 8 নিয়ে আজকের পর্বে আমরা আলোচনা করব ।
নিচের প্রশ্নগুলির উত্তর লেখ :
1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQ)
(i) বাস্তব সহগ যুক্ত একচলবিশিষ্ট দ্বিঘাত সমীকরণটি হল
(a) $x\left( {{x}^{2}}-1 \right)-3x=0$
(b) ${{x}^{2}}({{x}^{2}}-1)-6x=0$
(c) x(x-1)-x=0
(d) $2x-4=0$
উত্তর: (c) $x(x-1)-x=0$
(ii) (2x-2)(x+3)=0 সমীকরণটির বীজ দুটি হলো
(a) -1,-3
(b) -1,3
(c) 1,-3
(d) 1,3
উত্তর: (c) 1,-3
(iii) বার্ষিক 10% সরল সুদের হারে 50 টাকার 2 বছরের সুদ ঐ একই হারে 100 টাকার 1 বছরের সুদের
(a) দ্বিগুণ
(b) অর্ধেক
(c) এক চতুর্থাংশ
(d) সমান
উত্তর: (d) সমান
(iv) O কেন্দ্রীয় বৃত্তের PQ ও RS দুটি সমান দৈর্ঘ্যের জ্যা । O বিন্দু থেকে PQ জ্যা এর দূরত্ব 8 সেমি. হলে , O বিন্দু থেকে RS জ্যা এর দূরত্ব কত?
(a)8 সেমি
(b)16 সেমি
(c) 4 সেমি
উত্তর: (a) 8 সেমি ।
সমাধানঃ ত্রিভুজের কেন্দ্র থেকে জ্যা এর দূরত্ব বলতে লম্ব দূরত্ব বোঝায়। অর্থাৎ , $OC\bot PQ$ এবং $OD\bot RS$
OQ = OS (এরা একই বৃত্তের ব্যাসার্ধ)
$CQ=\frac{1}{2}PQ=\frac{1}{2}RS=DS$ (PQ ও RS দুটি সমান দৈর্ঘ্যের জ্যা)
$\vartriangle COQ$ ও $\vartriangle ODS$ এর
$\angle OCQ=ODS=90{}^\circ $
OQ=OS
CQ=DS
$\therefore $ $\vartriangle COQ$ ও $\vartriangle ODS$ পরস্পর সর্বসম।
$\therefore $ OC=OD=8 সেমি ।
(v) O কেন্দ্রীয় বৃত্তের বহিঃস্থ P বিন্দু থেকে অঙ্কিত স্পর্শক বৃত্তকে Q বিন্দুতে স্পর্শ করে। OQ = 9cm, PO = 15 সেমি. হলে PQ-এর দৈর্ঘ্য হবে
(a) 6 সেমি
(b) $\sqrt{{{15}^{2}}-{{9}^{2}}}$ সেমি
(c) $\sqrt{{{15}^{2}}+{{9}^{2}}}$ সেমি
(d) 13 সেমি
উত্তর: (b) $\sqrt{{{15}^{2}}-{{9}^{2}}}$ সেমি
(vi) দুটি নিরেট গোলকের বরুতলের ক্ষেত্রফলের অনুপাত 25 : 16 হলে, তাদের আয়তনের অনুপাত হবে
(a) 5 : 4
(b) 64 : 125
(c) 4 : 5
(d) 125 : 64
উত্তর: (d) 125 : 64
(vii) দুটি বৃত্ত পরস্পরকে C বিন্দুতে বহিঃস্পর্শ করে। AB বৃত্ত দুটির একটি সাধারণ স্পর্শক বৃত্তদুটিকে A ও B বিন্দুতে স্পর্শ করে, \$angle ACB$ -এর পরিমাপ হলো,
(a) 60°
(b) 45°
(c) 30°
(d) 90°
উত্তরঃ (d) 90°
(viii) একটি নিরেট অর্ধগোলকের সমগ্রতলের ক্ষেত্রফল $147\pi $ বর্গসেমি. হলে, উহার ব্যাসার্ধ হবে,
(a) 6 সেমি.
(b) 12 সেমি,
(c) 7 সেমি.
(d) 14 সেমি.।
উত্তরঃ (c) 7 সেমি.
2. সত্য / মিথ্যা লেখ (T/F)
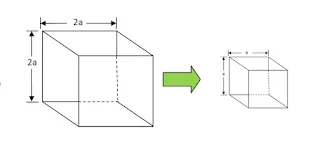
(i) একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য অর্ধেক করা হলে , ঘনকটির আয়তন প্রথম আয়তনের $\frac{1}{8}$ অংশ হবে।
উত্তর: সত্য (T) ।
সমাধানঃ
ধরি ঘনকটির প্রাথমিক বাহুর দৈর্ঘ্য ছিল 2a । অর্থাৎ অন্তিম দৈর্ঘ্য ছিল a ।
আমরা জানি , ঘনকের আয়তন = (বাহু)3
অতএব, প্রাথমিক আয়তন= (2a)3 = 8a3
এবং , অন্তিম আয়তন =(a)3 = a3
এখন,( অন্তিম আয়তন ÷ প্রাথমিক আয়তন) = $\frac{{{a}^{3}}}{8{{a}^{3}}}=\frac{1}{8}$
(ii) $\frac{a}{2}=\frac{b}{3}=\frac{c}{4}$ হলে , a:b:c=4:3:2 হবে।
উত্তর: মিথ্যা (T)।
সমাধানঃ
ধরি, $\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k$
বা, a=2k , b=3k , c=4k
এখন, a:b:c=2k:3k:4k = 2:3:4
(iii) আসল P টাকা এবং বার্ষিক চক্রবৃদ্ধি সুদের হার r% হলে , দ্বিতীয় বছরের মূলধন $\frac{Pr}{100}$ টাকা।
উত্তর: মিথ্যা (T) ।
সমাধান, দ্বিতীয় বছরের মূলধন =আসল + প্রথম বছরের সুদ।
দ্বিতীয় বছরের মূলধন = $P{{\left( 1+\frac{r}{100} \right)}^{1}}$
= $P+\frac{Pr}{100}\ne \frac{Pr}{100}$ ( কারণ , $P\ne 0$ )
(iv) চিত্রে O কেন্দ্রবিশিষ্ট বৃত্তে AB একটি ব্যাস । বৃত্তের ভেতরে Q একটি বিন্দু । $\angle AQB$ সর্বদা সূক্ষ্মকোণ ।
উত্তর: মিথ্যা (T) ।
সমাধান:
অঙ্কনঃ AQ কে বর্ধিত করলাম যা বৃত্তের পরিধিকে K বিন্দুতে ছেদ করল। R,B যুক্ত করলাম ।
প্রমাণঃ $\angle ARB=90{}^\circ $ ( অর্ধবৃত্তস্থ কোন)
$\therefore \angle RQB+\angle RBQ=90{}^\circ $
$\therefore \angle RQB=90{}^\circ -\angle RBQ$
$\therefore \angle RQB<90{}^\circ $ ($\angle RBQ\ne 0$)
$\therefore \angle AQB=180{}^\circ -\angle RQB$
$\therefore \angle AQB>90{}^\circ $ (প্রমাণিত)
(v) ∆ABC-এর BC বাহুর উপর D এমন একটি বিন্দু যে $AD\bot BC$। সুতরাং $\vartriangle ABD~\sim \vartriangle CAD$
উত্তর: মিথ্যা ।
(vi) শুভেন্দু ও নৌসদ যথাক্রমে 1500 টাকা এবং 1000 টাকা দিয়ে একটি ব্যবসা শুরু করে। এক বছর পরে ব্যবসায় 75 টাকা ক্ষতি হলে, শুভেন্দুর ক্ষতি হয় 30 টাকা।
উত্তর: মিথ্যা ।
(vii)
পাশের চিত্রে ST || QR হলে, $\frac{PQ}{PS}=\frac{PR}{PT}$ হবে।
উত্তর – বিবৃতিটি সত্য (T) ।
(viii) শঙ্কুর তির্যক উচ্চতার দ্বিগুণ হলে শঙ্কুর ব্যাসার্ধ হবে উচ্চতা ×$\sqrt{3}$
উত্তর - বিবৃতিটি সত্য (T) ।
3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (SA):
(i) একটি লম্ববৃত্তাকার চৌঙের আয়তন এবং বক্রতলের ক্ষেত্রফল সংখ্যামানে সমান হলে , উহার ব্যাসার্ধ নির্ণয় কর।
সমাধানঃ
লম্ব বৃত্তাকার চৌঙের আয়তন $=\pi {{r}^{2}}h$
লম্ব বৃত্তাকার চৌঙের বক্রতলের ক্ষেত্রফল $=2\pi rh$
শর্তানুসারে, $\not{\pi }{{r}^{2}}\not{h}=2\not{\pi }r\not{h}$
বা, $\frac{{{r}^{2}}}{r}$=2
বা, r = 2
উত্তরঃ চৌঙটির ব্যাসার্ধ 2 একক ।
(ii) দেখাও যে, মিশ্র দ্বিঘাত করণী $(7-\sqrt{2})$ এর অনুবন্ধী করণী হলো $(7+\sqrt{2})$ ।
সমাধানঃ
কোনো করণী ও তার অনুবন্ধী করণীর গুনফল সর্বদা একটি মুলদ সংখ্যা হবে।
এক্ষেত্রে, $(7-\sqrt{2})(7+\sqrt{2})$
= ${{7}^{2}}-{{(\sqrt{2})}^{2}}$=49-2 =47
অতএব $(7-\sqrt{2})$ এর অনুবন্ধী করণী হলো $(7+\sqrt{2})$ ।
(iii) একটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 12 সেমি এবং আয়তন $100\pi $ ঘন সেমি হলে, শঙ্কুটির ব্যাসার্ধের দৈর্ঘ্য কত তা নির্ণয় করো।
সমাধানঃ
ধরি শঙ্কুটির ব্যাসার্ধের দৈর্ঘ্য = r সেমি ।
লম্ব বৃত্তাকার শঙ্কুর উচ্চতা (h) = 12 সেমি
আয়তন = $100\pi $ ঘন সেমি
শর্তানুসারে , $\frac{1}{3}\pi {{r}^{2}}h=100\pi $
বা, $\frac{1}{3}\not{\pi }{{r}^{2}}\times 12=100\not{\pi }$
বা, ${{r}^{2}}=\frac{\overset{25}{\mathop{\not{1}\not{0}\not{0}}}\,\times \not{3}}{\underset{{\not{4}}}{\mathop{\not{1}\not{2}}}\,}$
বা, r = 5
উত্তরঃ শঙ্কুটির ব্যাসার্ধের দৈর্ঘ্য 5 সেমি ।
(iv) x $\propto $ yz এবং y $\propto $ zx হলে, দেখাও যে, z একটি অশূন্য ধ্রুবক।
সমাধানঃ $x~\propto yz$
বা, $x~={{k}_{1}}yz$--- (i) [$k{}_{1}$হলো অশুন্য ভেদ ধ্রুবক]
আবার, $y~\propto zx$
বা, $y={{k}_{2}}zx$--- (ii) [$k{}_{2}$হলো অশুন্য ভেদ ধ্রুবক]
(i) নং ও (ii) নং সমিকরন গুন করে পাই ,
$xy={{k}_{1}}yz\times {{k}_{2}}zx$
বা, $xy={{k}_{1}}.{{k}_{2}}.xy{{z}^{2}}$
বা, $\frac{xy}{{{k}_{1}}.{{k}_{2}}.xy}={{z}^{2}}$
বা, ${{z}^{2}}=\frac{\not{x}\not{y}}{{{k}_{1}}.{{k}_{2}}.\not{x}\not{y}}$
বা, ${{z}^{2}}=\frac{1}{{{k}_{1}}{{k}_{2}}}$
বা, $z=\sqrt{\frac{1}{{{k}_{1}}{{k}_{2}}}}$
বা, $z=\pm \sqrt{\frac{1}{{{k}_{1}}{{k}_{2}}}}$ [ একটি অশূন্য ধ্রুবক ]
(v) তিন বন্ধু A, B এবং C একসঙ্গে কিছু মূলধন নিয়ে একটি বাস ক্রয় করেন। তারা ঠিক করেন যে মোট আয়ের $\frac{2}{5}$ অংশ কাজের জন্য 3:2:2 অনুপাতে ভাগ করে নেবেন। কোনো একমাসে যদি 29260 টাকা আয় হয় তাহলে কাজের জন্য A-এর আয় B-এর আয় থেকে কত বেশি হবে?
উত্তর –
একমাসে মোট আয় হয় = 29260 টাকা।
আয়ের $\frac{2}{5}$টাকা =$29260\times \frac{2}{5}$টাকা = 11704 টাকা
A এর আয় , B এর আয়ের চেয়ে 11704 টাকার $\frac{(3-2)}{3+2+2}$অংশ = $\frac{1}{7}$বেশি ।
A এর আয় , B এর আয়ের চেয়ে $11704\times \frac{1}{7}$টাকা বেশি = 1672 টাকা বেশি ।
(vi) একটি লম্ব বৃত্তাকার চোঙ এবং লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 3:4 এবং তাদের আয়তনের অনুপাত 9:8; চোঙ ও শঙ্কুর উচ্চতার অনুপাত নির্ণয় করো।
উত্তর – ধরি ,
লম্ববৃত্তাকার চোঙের উচ্চতা ${{h}_{1}}$একক এবং ব্যাসার্ধ ${{r}_{1}}$একক ।
আবার ধরি , শঙ্কুর উচ্চতা ${{h}_{2}}$একক এবং ব্যাসার্ধ ${{r}_{2}}$একক ।
∴ চোঙের আয়তন = $\pi r_{1}^{2}{{h}_{1}}$ একক।
∴ শঙ্কুর আয়তন = $\frac{1}{3}\pi r_{2}^{2}{{h}_{2}}$ একক
প্রথম শর্তে , ${{r}_{1}}:{{r}_{2}}=3:4$
বা, $\frac{{{r}_{1}}}{{{r}_{2}}}=\frac{3}{4}$
দ্বিতীয় শর্তে , $\pi r_{1}^{2}{{h}_{1}}:\frac{1}{3}\pi r_{2}^{2}{{h}_{2}}=9:8$
বা, $\frac{\not{\pi }r_{1}^{2}{{h}_{1}}}{\frac{1}{3}\not{\pi }r_{2}^{2}{{h}_{2}}}=\frac{9}{8}$
বা , $\frac{3r_{1}^{2}{{h}_{1}}}{r_{2}^{2}{{h}_{2}}}=\frac{9}{8}$
বা , $\frac{{{r}_{1}}^{2}}{{{r}_{2}}^{2}}\times \frac{{{h}_{1}}}{{{h}_{2}}}=\frac{\overset{3}{\mathop{{\not{9}}}}\,}{8\times \not{3}}$
বা , ${{\left( \frac{{{r}_{1}}}{{{r}_{2}}} \right)}^{2}}\times \frac{{{h}_{1}}}{{{h}_{2}}}=\frac{\overset{3}{\mathop{{\not{9}}}}\,}{8\times \not{3}}$
বা, ${{\left( \frac{3}{4} \right)}^{2}}\times \frac{{{h}_{1}}}{{{h}_{2}}}=\frac{9}{8\times 3}$
বা, $\frac{{{h}_{1}}}{{{h}_{2}}}=\frac{{\not{9}}}{\not{8}\times 3}\times \frac{\overset{2}{\mathop{\not{1}\not{6}}}\,}{{\not{9}}}=\frac{2}{3}$
বা, ${{h}_{1}}:{{h}_{2}}=2:3$
(vii) যদি $y\propto {{x}^{3}}$ এবং $y\propto {{x}^{3}}$ এবং y-এর বৃদ্ধি 8:27 অনুপাতে হলে x-এর বৃদ্ধি কী অনুপাতে হয় তা নির্ণয় করো।
উত্তর –$y\alpha {{x}^{3}}$এবং y এর বৃদ্ধি 8:27
∴ $y=k.{{x}^{3}}$---(i) [ k হল অশুন্য ভেদ ধ্রুবক ]
ধরি যখন y এর বৃদ্ধি , ${{y}_{1}}=8a$ তখন x এর বৃদ্ধি ${{x}_{1}}$
আবার, যখন y এর বৃদ্ধি , ${{y}_{2}}=27a$ তখন x এর বৃদ্ধি ${{x}_{2}}$
(i) নং সমিকরন থেকে পাই ,
$y=k.{{x}^{3}}$
বা, ${{y}_{1}}=k.{{x}_{1}}^{3}$
বা, $8a=k.{{x}_{1}}^{3}---(ii)$
আবার, $y=k.{{x}^{3}}$
বা, ${{y}_{2}}=k.{{x}_{2}}^{3}$
বা, $27a=k.{{x}_{2}}^{3}---(iii)$
এখন , $(ii)\div (iii)$ করে পাই ,
$\frac{8\not{a}}{27\not{a}}=\frac{\not{k}.{{x}_{1}}^{3}}{\not{k}.{{x}_{2}}^{3}}$
বা, ${{\left( \frac{2}{3} \right)}^{3}}={{\left( \frac{{{x}_{1}}}{{{x}_{2}}} \right)}^{3}}$
বা, $\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{2}{3}$
বা, ${{x}_{1}}:{{x}_{2}}=2:3$
উত্তর : x এর বৃদ্ধি 2:3 অনুপাতে হয় ।
সমাধানঃ
প্রদত্ত: O কেন্দ্রীয় বৃত্তে PQRS একটি বৃত্তস্থ চতুর্ভুজ।
প্রমান্য বিষয়ঃ $\angle PQR+\angle PSR$ =2 সমকোণ ।
অঙ্কনঃ P , O এবং R , O যুক্ত করলাম।
প্রমাণঃ PSR বৃত্তচাপের দ্বারা গঠিত কেন্দ্রস্থ প্রবৃদ্ধ কোণ $\angle POR$ এবং বৃত্তস্থ কোণ $\angle PQR$
$\therefore $ প্রবৃদ্ধ $\angle POR$ =2$\angle PQR$
$\therefore \angle PQR=\frac{1}{2}$ প্রবৃদ্ধ $\angle POR$ …. (i)
আবার , PQR দ্বারা গঠিত কেন্দ্রস্থ প্রবৃদ্ধ কোণ $\angle POR$ এবং বৃত্তস্থ কোণ $\angle PSR$
$\therefore $ প্রবৃদ্ধ $\angle POR$ =2$\angle PSR$
$\therefore \angle PSR=\frac{1}{2}\angle POR$ …. (ii)
(i) ও (ii) থেকে পাই , $\angle PQR+\angle PSR$ = $\frac{1}{2}$ প্রবৃদ্ধ $\angle POR$$+\frac{1}{2}\angle POR$
= $\frac{1}{2}\times $ 4 সমকোণ = 2 সমকোণ। ( প্রমাণিত )
4.ii) যুক্তি দিয়ে প্রমাণ করো যে, বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে বহিঃস্থ বিন্দুর সংযোজক সরলরেখাংশ দুটির দৈর্ঘ্য সমান এবং তারা কেন্দ্রে সমান কোণ উৎপন্ন করে।
উত্তর – পাঠ্য বই এর পেজ ২১১ ( উপপাদ্য 41 )
5. (i) বার্ষিক 4% সরলসুদে কত বছরে 600 টাকার সুদ 168 টাকা হবে তা নির্ণয় করো।
সমাধান:
এক্ষেত্রে,
আসল (P) = 600 টাকা
সুদের হার (r) = 4% ( বার্ষিক )
সুদের পরিমান (I) = 168 টাকা
সময় (t) = ?
আমরা জানি , সুদের পরিমান (I) = $\frac{Ptr}{100}$
বা, $100I=Ptr$
বা, $t=\frac{100I}{\Pr }$
বা , t = $\frac{1\not{0}\not{0}\times \overset{\overset{7}{\mathop{\not{2}\not{8}}}\,}{\mathop{\not{1}\not{6}\not{8}}}\,}{\not{6}\not{0}\not{0}\times \not{4}}$বছর ।
নির্ণেয় সময় = 7 বছর ।
উত্তরঃ নির্ণেয় সময়ের পরিমান 7 বছর ।
(ii) কত টাকা বার্ষিক 5% চক্রবৃদ্ধিহার সুদে 2 বছর পরে সুদে আসলে 3528 টাকা হবে।
সমাধান:
এক্ষেত্রে,
ধরি আসল (P) = x টাকা ।
চক্রবৃদ্ধি সুদের হার (r) = 5% ( বার্ষিক )
সময় (n) = 2 বছর
সুদে আসলে (A) = 3528 টাকা
আমরা জানি ,
$A=P{{\left( 1+\frac{r}{100} \right)}^{n}}$
বা, 3528=$P{{\left( 1+\frac{5}{100} \right)}^{2}}$
বা, 3528 = $P{{\left( \frac{105}{100} \right)}^{2}}$
বা,P= $\frac{\overset{\overset{8}{\mathop{\not{1}\not{6}\not{8}}}\,}{\mathop{\not{3}\not{5}\not{2}\not{8}}}\,\times 100\times \overset{\overset{4}{\mathop{\not{2}\not{0}}}\,}{\mathop{\not{1}\not{0}\not{0}}}\,}{\underset{\not{2}\not{1}}{\mathop{\not{1}\not{0}\not{5}}}\,\times \underset{\not{2}\not{1}}{\mathop{\not{1}\not{0}\not{5}}}\,}$
বা , P=3200
উত্তরঃ নির্ণেয় টাকার পরিমানা 3200 টাকা ।