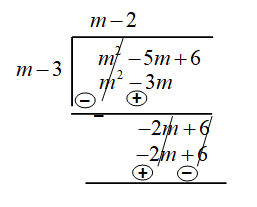Class 8 model activity task mathematics part 8 বা অষ্টম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট ৮ 2021 এর সমস্ত প্রশ্ন উত্তর নিয়ে আজকের পর্বে আমরা আলোচনা করব।
নীচের প্রশ্নগুলির উত্তর লেখো :
1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs) :
(i) দুটি পরস্পরছেদী সরলরেখার একজোড়া বিপ্রতীপ কোণ পরস্পর পুরক কোণ হলে, অপর
জোড়া বিপ্রতীপ কোণ দুটির প্রত্যেকটির মান হবে
(a) 180°
(b) 45
(c) 90°
(d) 135°
উত্তরঃ (d) 135°
(ii) দূরত্ব স্থির থাকলে যদি গতিবেগ দ্বিগুণ হয় তাহলে সময়
(a)
অর্ধেক হবে
(b) দ্বিগুণ হবে।
(c) অপরিবর্তিত থাকবে
(d) তিনগুণ
হবে।
উত্তরঃ (a) অর্ধেক হবে
(iii) 20 জন একটি কাজ 8 দিন করে। 10 জন ওই কাজটির $\frac{1}{2}$ অংশ করবে
(a) 32 দিনে
(b) ৪ দিনে
(c) 10 দিনে
(d) 2 দিনে
উত্তরঃ
(b) ৪ দিনে
(iv) এক ধরনের পিতলে তামা ও দস্তার পরিমাণের অনুপাত 5:2 । এই ধরনের 28 কিগ্রা পিতলে তামা আছে
(a) 8 কিগ্রা
(b) 11.2 কিগ্রা
(c) 16.8 কিগ্রা
(d) 20 কিগ্রা
উত্তরঃ (d) 20 কিগ্রা
সমাধানঃ 28 কিগ্রা পিতলে তামা আছে মোট পিতলের $\frac{5}{5+2}$ অংশ ।
অতএব , তামা আছে = $\frac{28\times 5}{7}$ কিগ্রা = 20 কিগ্রা
(v) বুলু ও তথাগত একটি কাজ একা একা যথাক্রমে 20 দিনে ও 30 দিনে করতে পারে। দুজন একসঙ্গে 1 দিনে করে
(a) $\left( \frac{1}{2}+\frac{1}{3} \right)$ অংশ
(b) (20+30) অংশ
(c) $\left( \frac{1}{20}+\frac{1}{30} \right)$ অংশ
(d) $\left( \frac{1}{20}-\frac{1}{30} \right)$ অংশ
উত্তরঃ (c) $\left( \frac{1}{20}+\frac{1}{30} \right)$ অংশ
(vi)
চিত্রে , (a) QR<PR (b) PR<PQ (c) QR<PQ (d) QR>PQউত্তরঃ (d) QR>PQ
উত্তরের ব্যাখ্যা নিচের ভিডিওতেঃ
(vii) (2m+5n)(2m-5n) এবং mn(2m-5n) সংখ্যামালা দুটির গসাগু হল -
(a) 1
(b) mn(2m+5n)(2m-5n)
(c) (2m+5n)
(d) (2m-5n)
উত্তরঃ (d) (2m-5n)
2. সত্য/মিথ্যা লেখো (T/F):
(i) 30 লিটার ডেটল-জলে জল ও ডেটলের পরিমাণের অনুপাত 5:1, ইহাতে ডেটল আছে
25 লিটার।
উত্তরঃ মিথ্যা।
(ii) ($27{{x}^{3}}-343{{y}^{3}}$ )
সংখ্যামালাটি (3x - 7y) দ্বারা বিভাজ্য।
উত্তরঃ সত্য ।
(iii)
$2{{a}^{2}}b$ এবং $4a{{b}^{2}}$ -এর গ.সা.গু হলো 4a2b2
উত্তরঃ মিথ্যা।
(iv) $\frac{{{x}^{2}}}{a}+\frac{{{a}^{2}}}{x}=\frac{{{x}^{2}}+{{a}^{2}}}{a+x}$.
উত্তরঃ মিথ্যা।
(v)
চিত্রে x° = 70°-50°উত্তরঃ মিথ্যা ।
ব্যাখ্যাঃ চিত্রে x° = 70°+59° = 129° হবে ।
(vi) হারুনচাচা 1 দিনে কোনো কাজের $\frac{1}{10}$অংশ করেন । সম্পূর্ণ কাজটি করতে হারুনচাচার 10 দিন সময় লাগবে।
(vii) 2.25 টাকা, – 5 টাকার শতকরা 4.5
উত্তরঃ মিথ্যা ।
সঠিক উত্তর হবে - 2.25 টাকা, – 5 টাকার শতকরা 45
3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন :
(i)
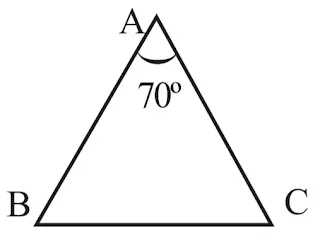
চিত্রে $\vartriangle ABC$ -এর AB=AC এবং $\angle BAC=70{}^\circ $ | $\angle ABC$ এবং $\angle ACB$ -এর পরিমাপ নির্ণয় করো।
সমাধানঃ
যেহেতু AB=AC , তাই $\angle ABC$ এবং $\angle ACB$ -এর পরিমাপ সমান ।
এখন, $\angle ABC+\angle ACB=180{}^\circ -70{}^\circ =110{}^\circ $
অর্থাৎ, $\angle ABC=\angle ACB=\frac{110}{2}{}^\circ =55{}^\circ $
(ii) দুটি সমান মাপের কৌটায় মিশ্র চায়ে আসাম চা ও দার্জিলিং চায়ের পরিমাণের অনুপাত যথাক্রমে 5:18 এবং 2:31 কোন কোটায় আসাম চায়ের পরিমাণ বেশী আছে?
সমাধানঃ
প্রথম কৌটায় আসাম চা আছে মোট চায়ের $\frac{5}{5+18}$ অংশ $=\frac{5}{23}$ অংশ
দ্বিতীয় কৌটায় আসাম চা আছে মোট চায়ের $\frac{2}{2+31}$ অংশ $=\frac{2}{33}$ অংশ
তুলনা করিঃ
$\therefore \ \,\frac{5}{23}\quad ,\quad \frac{2}{33}$
$\therefore \ \,\frac{5\times 33\quad ,\quad 2\times 23}{23\times 33}$
$\therefore \ \,\frac{165\quad >\quad 46}{23\times 33}$
উত্তরঃ প্রথম কৌটায় আসাম চা এর পরিমাণ বেশী ।
(iii) গনিতের ভাষায় সমস্যাটি হল
| গরুর সংখ্যা (টি) | সময় (দিন) | খড়ের পরিমাণ (কাহন) |
|---|---|---|
| 8 | 15 | 4 |
| 10 | 72 | x |
(a) সময় স্থির থাকলে গোরুর সংখ্যার সঙ্গে খড়ের পরিমাণের সমানুপাত সম্পর্কটি লেখো। (b) গোরুর সংখ্যা স্থির থাকলে সময়ের সঙ্গে খড়ের পরিমাণের সমানুপাত সম্পর্কটি লেখো।
উত্তরঃ (a) সময় স্থির থাকলে গোরুর সংখ্যার সঙ্গে খড়ের পরিমাণের সমানুপাত সম্পর্কটি হবে সরল সমানুপাত।
(b) গোরুর সংখ্যা স্থির থাকলে সময়ের সঙ্গে খড়ের পরিমাণের সমানুপাত সম্পর্কটি হবে সরল সমানুপাত।
(iv) x2+px+q বীজগাণিতিক সংখ্যামালায় p=a+b এবং q=a×b হলে, সংখ্যামালাটির উৎপাদক দুটি লেখো।
সমাধানঃ ${{x}^{2}}+px+q$
$={{x}^{2}}+(a+b)x+ab$ [ কারন p=a+b এবং q=a×b]
$={{x}^{2}}+ax+bx+ab$
$=x(x+a)+b(x+a)$
$=(x+a)(x+b)$
4. (i) $\frac{x}{2}=\frac{1}{2x}+1$ হলে , $\left( {{x}^{3}}-\frac{1}{{{x}^{3}}} \right)$- এর মান নির্ণয় করো।
সমাধানঃ
$\frac{x}{2}=\frac{1}{2x}+1$
বা, $\frac{x}{2}-\frac{1}{2x}=1$
বা, $x-\frac{1}{x}=2$ [ উভয় পক্ষকে 2 দ্বারা গুন করে ]
প্রদত্ত $\left( {{x}^{3}}-\frac{1}{{{x}^{3}}} \right)$
= ${{\left( x-\frac{1}{x} \right)}^{3}}+3.\not{x}.\frac{1}{{\not{x}}}\left( x-\frac{1}{x} \right)$
= ${{\left( 2 \right)}^{3}}+3\times 2$
=8+6
= 14
অন্যভাবে সমাধান:
সমাধান: $\frac{x}{2}=\frac{1}{2x}+1$
বা, $x=\frac{1}{x}+2$
বা, $x-\frac{1}{x}=2$
এখন , ${{x}^{3}}-\frac{1}{{{x}^{3}}}$
= $\left( x-\frac{1}{x} \right)\left\{ {{x}^{2}}+x.\frac{1}{x}+{{\left( \frac{1}{x} \right)}^{2}} \right\}$
$=\left( x-\frac{1}{x} \right)\left\{ {{x}^{2}}-2\not{x}.\frac{1}{{\not{x}}}+{{\left( \frac{1}{x} \right)}^{2}}+3\not{x}.\frac{1}{{\not{x}}} \right\}$
$=\left( x-\frac{1}{x} \right)\left\{ {{\left( x-\frac{1}{x} \right)}^{2}}+3 \right\}$
= $2\times ({{2}^{2}}+3)$
= $2\times (4+3)=2\times 7=14$
(ii) ভাগ করো $\left( {{m}^{2}}-5m+6 \right)$ -কে (m - 3) দিয়ে
উত্তর: নির্ণেয় ভাগফল (m-2) ।
5. ক্লাসের ছাত্রছাত্রীরা কোন কোন খেলা কতজন করে পছন্দ করে শতকরায় তার তালিকা হলো ( একজন কেবলমাত্র একটি খেলাই পছন্দ করবে )
| খেলা | খেলা পছন্দ করা ছাত্র-ছাত্রীর সংখ্যা (শতকরায়) |
|---|---|
| ক্রিকেট | 60 |
| ফুটবল | 30 |
| ব্যাডমিন্টন | 10 |
পাই চিত্রে, যে বৃত্তকলাগুলি তথ্যটির অংশগুলিকে বোঝাবে সেই বৃত্তকলাগুলির কেন্দ্রীয় কোণগুলি নির্ণয় করো এবং তথ্যটির পাই চিত্র অঙ্কন করো ।
সমাধানঃ
পাইচিত্রের মোট কেন্দ্রীয় কোণ 360°
ক্রিকেট নির্দেশক বৃত্তকলার কেন্দ্রীয় কোণ $=360\times \frac{60}{60+30+10}$ °
= $36\not{0}\times \frac{6\not{0}}{1\not{0}\not{0}}$ ° = 216°
ফুটবল নির্দেশক বৃত্তকলার কেন্দ্রীয় কোণ $=36\not{0}\times \frac{3\not{0}}{1\not{0}\not{0}}$ ° = 108°
ব্যাডমিন্টন নির্দেশক বৃত্তকলার কেন্দ্রীয় কোণ $=36\not{0}\times \frac{1\not{0}}{1\not{0}\not{0}}$ ° = 36°
6. (i) যুক্তি দিয়ে প্রমাণ করো যে, ত্রিভুজের কোনো একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয় সেটির পরিমাপ অন্তঃস্থ বিপরীত কোণ দুটির পরিমাপের যোগফলের সমান।
[Ans source : Textbook page 145]
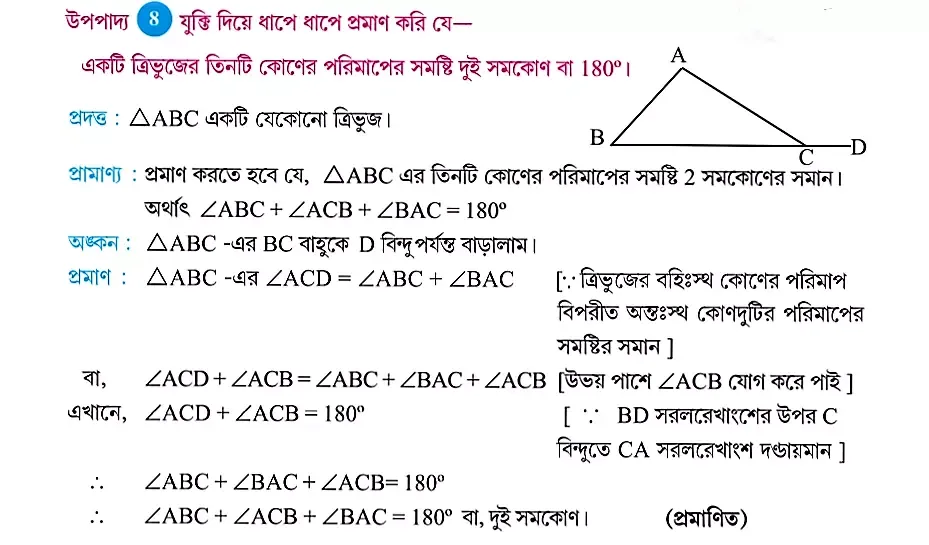
6. (ii) প্রমান করবে, যে কোনো ত্রিভুজের তিনটি কোণের সমষ্টি 180°
[Ans source : Textbook page 147]
7. 5 অশ্বক্ষমতাসম্পন্ন একটি পাম্প 36000 লিটার জল ৪ ঘণ্টায় উপরে তুলতে পারে। 7 অশ্বক্ষমতা সম্পন্ন পাম্পের 63000 লিটার জল তুলতে কত সময় লাগবে ত্রৈরাশিক পদ্ধতিতে নির্ণয় করো।
সয়ামধানঃ
গনিতের ভাষায় সমস্যা টি হল -
| পাম্পের ক্ষমতা (অশ্বক্ষমতা) | জল (লিটার) | সময় (ঘন্টা) |
|---|---|---|
| 5 | 36000 | 8 |
| 7 | 63000 | ? |
এক্ষেত্রে জলের পরিমান স্থির থাকলে পাম্পের ক্ষমতা বাড়লে সময় কম লাগে অর্থাৎ পাম্পের ক্ষমতা ও সময়ের মধ্যে ব্যস্ত সম্পর্ক।
আবার পাম্পের ক্ষমতা স্থির থাকলে জলের পরিমান বাড়লে সময় বেশি লাগে । অর্থাৎ জলের পরিমান ও সময়ের মধ্যে সরল সম্পর্ক।
নির্ণেয় সময় = $8\times \frac{5}{{\not{7}}}\times \frac{\overset{9}{\mathop{\not{6}\not{3}}}\,\not{0}\not{0}\not{0}}{36\not{0}\not{0}\not{0}}$ঘণ্টা
= $8\times \frac{5}{{\not{7}}}\times \frac{\overset{{\not{9}}}{\mathop{\not{6}\not{3}}}\,\not{0}\not{0}\not{0}}{\underset{4}{\mathop{\not{3}\not{6}}}\,\not{0}\not{0}\not{0}}$ঘণ্টা
= $\overset{2}{\mathop{{\not{8}}}}\,\times \frac{5}{{\not{7}}}\times \frac{\overset{{\not{9}}}{\mathop{\not{6}\not{3}}}\,\not{0}\not{0}\not{0}}{\underset{{\not{4}}}{\mathop{\not{3}\not{6}}}\,\not{0}\not{0}\not{0}}$ঘণ্টা
= 10 ঘণ্টা
আরও দেখো: অষ্টম শ্রেণীর ভূগোল মডেল অ্যাক্টিভিটি টাস্ক part-1 2022