দশম শ্রেণী গণিত মডেল অ্যাক্টিভিটি টাস্ক পার্ট 5
নীচের প্রশ্নগুলির উত্তর লেখো :
1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs) :
(i) দুটি পরস্পরছেদী সরলরেখার
একজোড়া বিপ্রতীপ কোণ পরস্পর পুরক কোণ হলে, অপর জোড়া বিপ্রতীপ কোণ দুটির
প্রত্যেকটির মান হবে
(a) 180°
(b) 45
(c) 90°
(d)
135°
উত্তরঃ (d) 135°
(ii) দূরত্ব স্থির থাকলে যদি গতিবেগ দ্বিগুণ হয় তাহলে সময়
(a) অর্ধেক
হবে
(b) দ্বিগুণ হবে।
(c) অপরিবর্তিত থাকবে
(d) তিনগুণ হবে।
উত্তরঃ
(a) অর্ধেক হবে
(iii) 20 জন একটি কাজ 8 দিন করে। 10 জন ওই কাজটির $\frac{1}{2}$ অংশ করবে
(a)
32 দিনে
(b) ৪ দিনে
(c) 10 দিনে
(d) 2 দিনে
উত্তরঃ (b) ৪
দিনে
(iv) 80 টাকার 5% =
(a) 400 টাকা
(b) 16 টাকা
(c) 4 টাকা
(d)
400%
উত্তরঃ (c) 4 টাকা
2. সত্য/মিথ্যা লেখো (T/F):
(i) 30 লিটার ডেটল-জলে জল ও ডেটলের পরিমাণের
অনুপাত 5:1, ইহাতে ডেটল আছে 25 লিটার।
উত্তরঃ মিথ্যা।
(ii)
($27{{x}^{3}}-343{{y}^{3}}$ ) সংখ্যামালাটি (3x - 7y) দ্বারা বিভাজ্য।
উত্তরঃ সত্য
।
(iii) $2{{a}^{2}}b$ এবং $4a{{b}^{2}}$ -এর গ.সা.গু হলো 4ab
উত্তরঃ
মিথ্যা।
(iv) $\frac{2xb}{4{{x}^{2}}}$ - এর লঘিষ্ঠ আকারে প্রকাশ হলো
$\frac{b}{2x}$
উত্তরঃ সত্য।
Class 8 Mathematics Model Activity Task part 5
3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন :
(i)
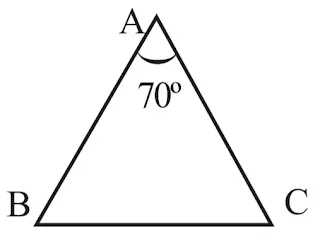
চিত্রে $\vartriangle ABC$ -এর AB=AC
এবং $\angle BAC=70{}^\circ $ | $\angle ABC$ এবং $\angle ACB$ -এর পরিমাপ
নির্ণয় করো।
সমাধানঃ
যেহেতু AB=AC , তাই $\angle ABC$ এবং $\angle
ACB$ -এর পরিমাপ সমান ।
এখন, $\angle ABC+\angle ACB=180{}^\circ
-70{}^\circ =110{}^\circ $
অর্থাৎ, $\angle ABC=\angle
ACB=\frac{110}{2}{}^\circ =55{}^\circ $
(ii) দুটি সমান মাপের কৌটায় মিশ্র চায়ে আসাম চা ও দার্জিলিং চায়ের পরিমাণের
অনুপাত যথাক্রমে 5:18 এবং 2:31 কোন কোটায় আসাম চায়ের পরিমাণ বেশী আছে?
সমাধানঃ
প্রথম কৌটায় আসাম চা আছে মোট চায়ের $\frac{5}{5+18}$ অংশ $=\frac{5}{23}$
অংশ
দ্বিতীয় কৌটায় আসাম চা আছে মোট চায়ের $\frac{2}{2+31}$ অংশ
$=\frac{2}{33}$ অংশ
তুলনা করিঃ
$\therefore \ \,\frac{5}{23}\quad
,\quad \frac{2}{33}$
$\therefore \ \,\frac{5\times 33\quad ,\quad
2\times 23}{23\times 33}$
$\therefore \ \,\frac{165\quad >\quad
46}{23\times 33}$
উত্তরঃ প্রথম কৌটায় আসাম চা এর পরিমাণ বেশী ।
ক্লাস এইট ম্যাথ মডেল অ্যাক্টিভিটি পার্ট 5
4. যুক্তি দিয়ে প্রমাণ করো যে, একটি ত্রিভুজের দুটি কোণের পরিমাপ সমান হলে, তাদের বিপরীত বাহুগুলির দৈর্ঘ্য সমান হবে।
প্রদত্ত: ত্রিভুজ ABC এর $\angle ABC=\angle ACB$
$\angle ABC$এর বিপরীত বাহু AC এবং $\angle ACB$ এর বিপরীত বাহু AB
প্রমাণ করতে হবে: AB = AC
অঙ্কন: $\angle BAC$ এর সমদ্বিখণ্ডক AD অঙ্কন করলাম যা BC কে D বিন্দুতে ছেদ
করে।
প্রমাণ: $\Delta ABD$ ও $\Delta ACD$ এর,
$\angle BAD=\angle CAD$
[ যেহেতু $\angle BAC$ এর সমদ্বিখণ্ডক হল AD ]
$\angle ABC=\angle ACB$ (
প্রশ্নে বলা আছে )
AD সাধারণ বাহু ।
অতএব , $\vartriangle ABD\cong
\vartriangle ACD$ [ A-A-S এর শর্ত অনুযায়ী ]
$\therefore $ AB=AC (
প্রমাণিত)